Generating Synthetic Financial Time Series
*** NEW ***
At Skanalytix we’ve put our money where our mouth is and have made our Synthetic Financial Time Series Generator available online for free.
Try our online financial time series generator
We’d love to know what you think!
Please send any comments or suggestions to: admin@skanalytix.com
Generating synthetic financial time series can be a valuable tool in various aspects of financial modeling and analysis. For example, trading strategy designers may want to test strategies under extreme conditions such as market crashes or other extreme events. But the problem is that there is limited historical data available, and this historical data will contain few examples of such extreme events. Synthetic data can be used to fill these gaps.
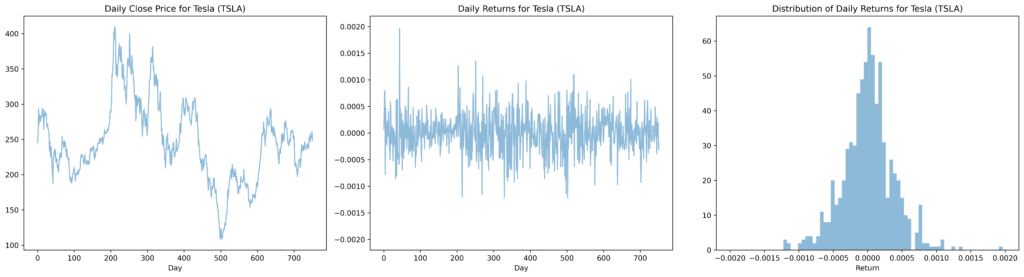
The challenge in generating synthetic ‘financial’ time series lies in the fact that most financial time series of interest exhibit stylized features including fat tails, volatility clustering and mean reversion. For example, consider Tesla (TSLA) prices over the period 1 Jan 2021 to 1 Jan 2024. The following figure shows the price series, the corresponding return series, and a histogram showing the distribution of returns. Mean reversion, volatility clustering, and fat-tails respectively can clearly be seen in the three plots.
While parametric models such as Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs) have become very popular in this space, their results have been inconsistent. These models often struggle to capture features such as volatility clustering and mean reversion. They also come with many practical challenges including training instability, high resource demands, and limited interpretability.
Like all Skanalytix tools, the Skanalytix Financial Time Series Generator is based on our UNCRi framework, which allows the probability distribution of returns to be estimated conditional on previous values of returns. The net result of this is that it can successfully capture the long-term dependencies inherent in stylized features such volatility clustering and mean reversion, thus generating ‘realistic’ financial time series. To boot, because it explicitly estimates conditional distributions, it is anything but a black box since these distributions can be directly visualized.
If you are interested in technical details, you can find more about how the Skanalytix synthetic financial time series generator operates in our Medium article titled ‘Generating Realistic Synthetic Financial Time Series‘. Below you will find some examples of using the Time Series Generator.
Daily close prices of Apple Inc (AAPL) from 1 Jan 2021 to 1 Jan 2024
The figure below shows prices series information for daily close prices of Apple Inc. shares (AAPL) on the NYSE for the 3-year period from 1 Jan 2021 to 1 Jan 2024. The top row corresponds to the historical series, the second and third rows to synthetic series generated by the UNCRi synthetic financial time series generator. From left to right, plots show (i) the return distribution; (ii) the returns series; (iii) the price series trajectory corresponding to the return series, (iv) the autocorrelation of returns plot (which indicates whether any serial correlation is present), and (v) the autocorrelation of absolute returns plot (which reflects the presence and degree of any volatility clustering that may be present).
Historical series
Synthetic series
It is informative to examine the PCA and t-SNE plots of the original and synthetic returns. These are handy dimensionality reduction techniques that allow us to visualize high-dimensional data in two dimensions. The figure below show the plots corresponding to the historical series and the first synthetic series above. Both methods show that points from the historical and synthetic datasets are well interspersed, indicating that the synthetic data captures a broad range of variability similar to the historical data. Moreover, there are no single-colored clusters, indicating that there are no patterns present in one group but absent in the other. We can be confident that the synthetic data has mimicked the overall structure of the historical data.
Daily close prices of S&P500 (^GSPC) from 1 Jan 2010 to 1 Jan 2020
In this case we consider a longer time period (10 years) and use an index (S&P500) as opposed to a single asset price. As above, we show the original series and two synthetic series. Both synthetic series display fat-tails and volatility clustering similar to the original series, and again, the evolution of prices is realistic and reflects the general exponential pattern of price increase present in the original series.
Historical series
Synthetic series
The fat tails and volatility clustering in the synthetic series closely reflects that present in the historical data, and there is no significant serial correlation present in either the historical or synthetic series. The two synthetic price trajectories are quite different to each other and to the historical price series, but they are both confined to a reasonable range, indicating that the mean reversion has been captured.
Multiple Correlated Time Series
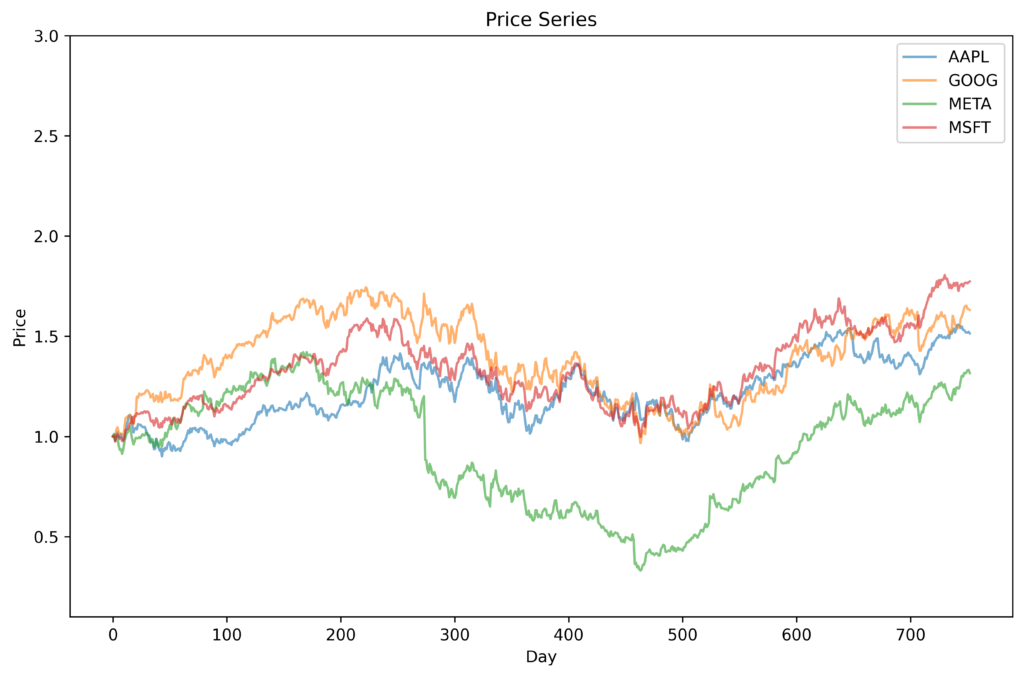
There are situations (e.g., portfolio management) in which it is necessary to consider the price series of multiple assets simultaneously. In many cases these asset prices will be correlated to some degree, either positively or negatively. So, it is important that the synthetic series derived from these are also correlated in the same way. Generating the series independently won’t work. However, the UNCRi framework is able to simultanously generate multiple correlated price series while maintaining the stylized features of each asset. The figure below show the original prices series and three synthetic price series for the tech stocks Apple (AAPL), Google (GOOG), Facebook (META) and Microsoft (MSFT) over the three-period from 1 Jun 2021 to 1 Jan 2024. The price changes of these stocks are strongly positively correlated with each other, as can be seen for the original price series. The synthetic series have clearly captured these correlations.
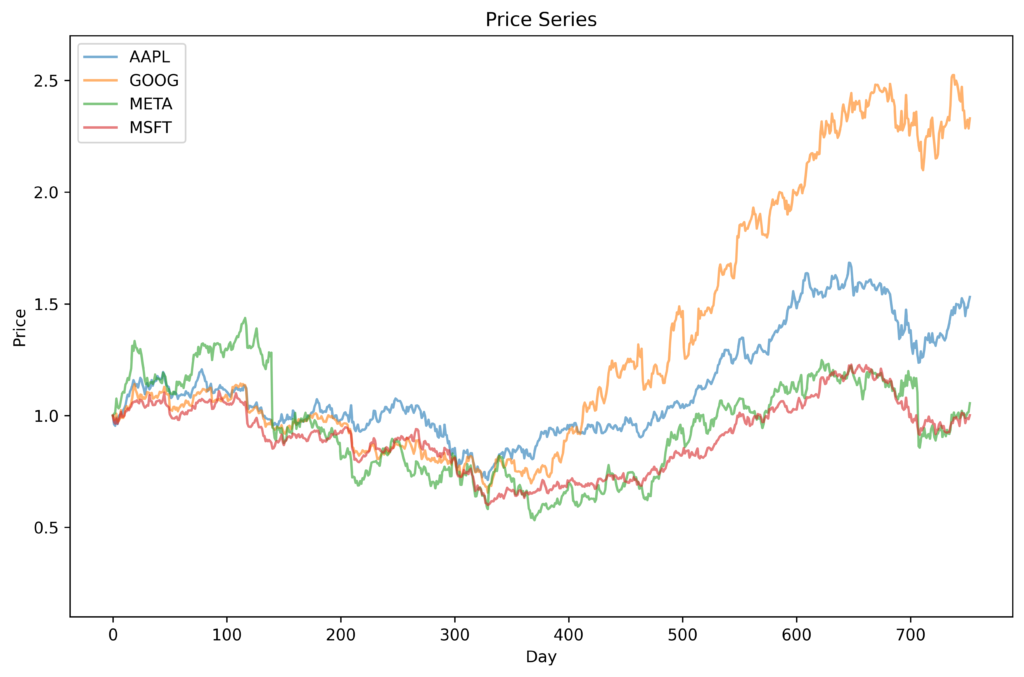
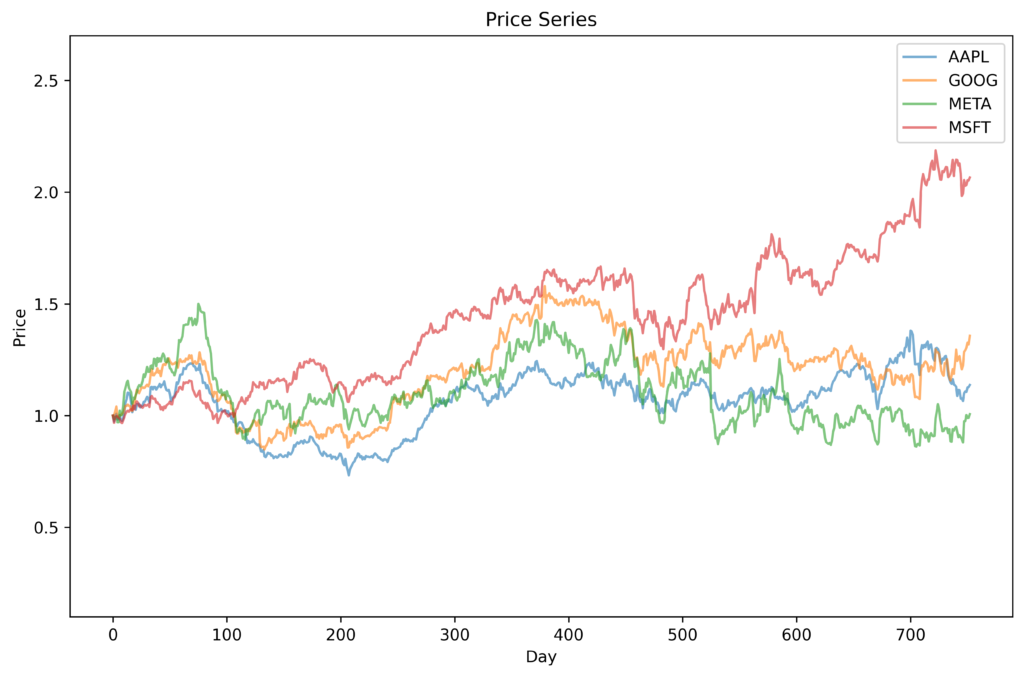
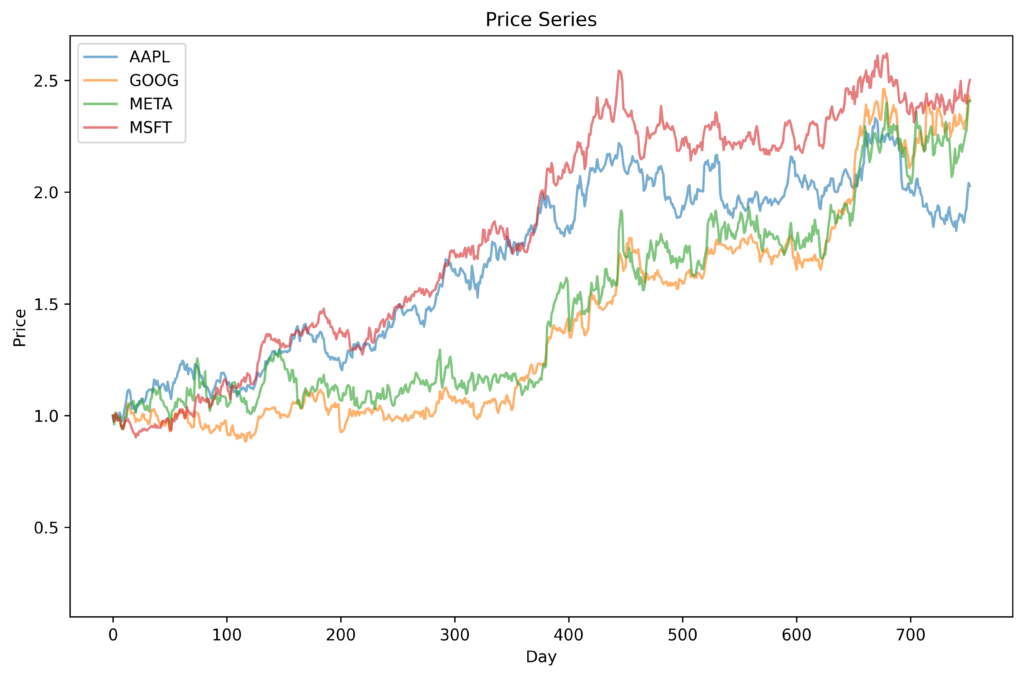
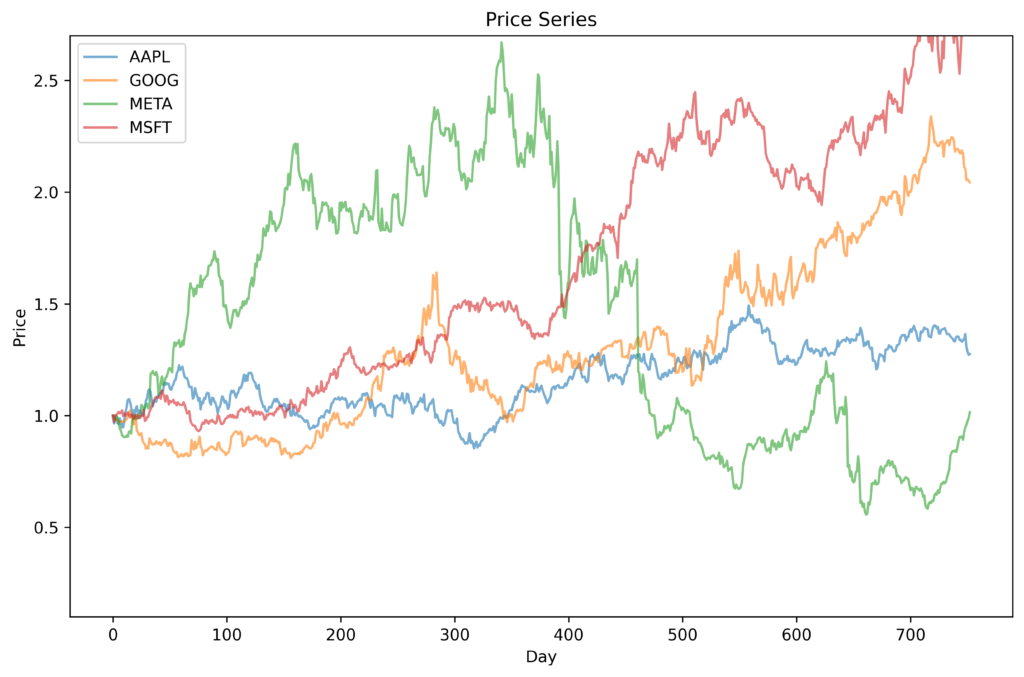
For comparison, the following figure shows synthetic prices trajectories for the same four companies, but WITHOUT correlations.
Conclusion
Financial time series often display stylized features such as fat tails, volatility clustering and mean reversion. To capture these features in a synthetic dataset it is not sufficient to model the unconditional distribution of returns; rather, one must be able to model the distribution of returns conditional on past values. The UNCRi framework has been designed specifically to model conditional probability distributions, and when applied to financial data is able to generate realistic time series which accurately reflect the stylized features present in the original series. It is also possible to use the framework to simultaneously generate multiple asset series which capture the correlations between those asset prices while at the same time maintaining the stylized features of the individual series.
The examples in this case study have been based on using only numerical input data, specifically lagged returns. However, the UNCRi framework is flexible, and it is possible to also include numeric or categorical features ‘auxiliary’ features, which might include fundamentals such as price/earning ratios, economic variables, sentiment, and so on.